Bayes Teoremi

Bayes teoremi, olasılığın temel yapıtaşlarından biridir. Adı, on sekizinci yüzyılda teoriyi öneren Thomas Bayes’ten (1702 – 1761) geliyor. Fakat bu bilim insanı tam olarak ne açıklamaya çalışıyordu? Meriam-Webster sözlüğüne göre, olasılık, “verilen bir olayı meydana getiren, eşit derecede olası sonuçların kapsamlı bir setindeki sonuç sayısının, olası sonuçların toplam sayısına oranıdır”.

Dünyayı yöneten birçok olasılık teorisi vardır. Örneğin, doktora gittiğinizde sizi iyileştirmesi en muhtemel olan ilacı belirler. Ayrıca, reklam verenler kampanyalarını, tanıtımını yaptıkları ürünü satın alma olasılıkları daha yüksek olan insanlara odaklar. Benzer şekilde, günlük işe geliş gidişiniz için, daha az zaman alması muhtemel bir rota seçersiniz.

Toplam olasılık yasası

En ünlü olasılık kanunlarından biri, toplam olasılık yasasıdır. Toplam olasılık yasasının ne olduğunu analiz etmek önemlidir. Bunu anlamak için size bir örnek vereceğiz.

Diyelim ki, rastgele bir ülkede, vatandaşların %39’u kadın. Ayrıca kadınların %22’sinin ve erkeklerin %14’ünün bir işi olmadığını da biliyoruz. Öyleyse, bu ülkedeki aktif nüfustan (P) rastgele seçilen bir kişinin işsiz P (U) olma olasılığı nedir?

Olasılık teorisine göre, bu olasılığı şöyle hesaplayabiliriz:

• Kişinin bir kadın olma olasılığı: P (K)
• Kişinin bir erkek olma olasılığı: P (E)

Vatandaşların %39’unun kadın olduğunu bildiğimiz için P (K) = 0,39 olduğunu tespit edebiliriz.

Böylece P (E) = 1 – 0,39 = 0,61 olduğunu söyleyebiliriz.

Ayrıca, belirtilen sorun bize koşullu olasılıkları da vermektedir:

• Bir kadının işsiz olma olasılığı: P (U | K) = 0,22
• Bir erkeğin işsiz olma olasılığı: P (U | E) = 0,14

Bu nedenle, toplam olasılık yasasını kullanarak şunları elde ederiz:

P (U) = P (K) P (U | K) + P (E) P (U | E)

P (U) = 0,22 × 0,39 + 0,14 × 0,61

P (U) = 0,17

Bu nedenle, rastgele seçilen bir kişinin P (U) işsiz olması ihtimali 0,17 olacaktır. Sonuçların iki koşullu olasılık arasında olduğunu görebilirsiniz (0,14 <0,17 <0,22).

Bayes teoremi

Şimdi, bir formu doldurmak için rastgele bir yetişkin seçtiğinizi ve onların iş sahibi olmadığını anladığınızı varsayalım. Bu durumda, önceki örneği de göz önüne alarak, rastgele seçtiğiniz kişinin bir kadın olma olasılığı nedir [P (K | U)]?

Bu sorunu çözmek için, Bayes teoremini uygulamanız gerekir. Spesifik olarak, bu teoremi, bir olayın olasılığını bu olayla ilgili daha önceki bilgilerinizi dikkate alarak hesaplamak için kullanırsınız. A olayının olasılığını, bu olayın olasılığını etkileyen belirli özellikleri (B) yerine getirdiğini bilerek de hesaplayabilirsiniz.

Bu durumda, formu doldurması için rastgele seçtiğiniz kişinin bir kadın olma ihtimalinden bahsediyoruz. Ayrıca, olasılık, kişinin bir işi olup olmamasından bağımsız olmayacaktır.

Bayes teoremi formülü

Diğer teoremler gibi, burada da olasılığı hesaplamak için bir formüle ihtiyacımız var:

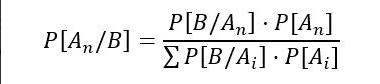
Her ne kadar zor gibi görünse de, formüldeki her şeyin bir açıklaması var:

• Öncelikle, B, önceden bilgi sahibi olduğumuz olaydır.
• Öte yandan, A (n) terimi farklı koşullu olayları ifade eder.
• Payda şartlı olasılık var. Bu, başka bir olayın (B olayının) da gerçekleştiğini bilerek bir olayın (A olayının) oluşma olasılığını ifade eder. Bunu P (A | B) olarak tanımlıyoruz ve ‘B olduğunda A’nın olasılığı’ olarak ifade ediyoruz.
• Paydada P (B)’nin eşiti bulunuyor.

Bir örnek

Önceki örneğe geri dönersek, bir anket doldurmak için rastgele bir yetişkin seçtiğinizi ve bir işlerinin olmadığını anladığınızı varsayalım. Bu kişinin bir kadın olma olasılığı nedir [P (K | U)]?

Önceki örnek göz önüne alındığında, aktif nüfusun %39’unun kadın olduğunu biliyoruz. O zaman biliyoruz ki gerisi erkek. Ayrıca, işsiz kadınların yüzdesinin %22 ve işsizlerin yüzdesinin %14 olduğunu biliyoruz.

Son olarak, rastgele, işsiz bir insan seçme olasılığımızın 0,17 olduğunu biliyoruz. Öyleyse, Bayes teoremini uygularsak, elde edeceğimiz sonuç, işsiz insanların arasından rastgele seçilen bir kişinin kadın olma ihtimalinin 0,5 olmasıdır.

P (K | U) = (P (K) * P (U | K) / P (U)) = (0,22 * 0,39) / 0,17 = 0,5

Bu makaleyi olasılıkla ilgili en sık rastlanan karışıklıklardan birine atıfta bulunarak bitireceğiz. Olasılık yalnızca 0 ile 1 arasında olabilir. Bir olayın olasılığı 0 ise, gerçekleşmesi imkansızdır. Öte yandan, olasılık 1 ise, o zaman kesinlikle gerçekleşecektir.